Пространственное (Intra) предсказание в HEVC

ГЛАВА 3

Пространственное предсказание (Intra). Обработка изображения в HEVC. Процедура пространственного предсказания: четыре этапа. Алгоритмы расчета значений пикселов внутри кодируемого блока.

Системы видеокодирования стандарта HEVC относятся к так называемым блочным гибридным кодекам. Блочность здесь означает, что каждый видеокадр во время кодирования разбивается на блоки, к которым и применяются алгоритмы видеокомпрессии. Что означает слово гибридный? Сжатие видеоданных при кодировании происходит во многом за счет устранения избыточности информации в последовательности видеоизображений. Очевидно, что изображения в соседних по времени видеокадрах с высокой вероятностью оказываются похожими друг на друга. При устранении временной избыточности для каждого кодируемого блока в текущем кадре ищется наиболее похожее изображение в ранее закодированных кадрах. Найденное изображение рассматривается как некоторая оценка (предсказание) кодируемого участка видеокадра. Результат предсказания вычитается из значений пикселов текущего блока. Разностный сигнал при «удачном» предсказании содержит значительно меньше информации, чем исходное изображение, что и обеспечивает эффективное сжатие. Но это только один из вариантов устранения избыточности. В HEVC предусмотрен и другой вариант, в котором для предсказания используются значения пикселов того же самого видеокадра, к которому относится кодируемый блок. Такое предсказание называют пространственным или внутрикадровым (Intra). Именно о наличии двух вариантов устранения временной или пространственной избыточности видеоизображений говорит слово гибридный.  Заметим также, что эффективность Intra-предсказания во многом определяет эффективность всей системы кодирования в целом. Рассмотрим более детально основные идеи методов и алгоритмов Intra-предсказания, предоставляемых стандартом HEVC.

Обработка изображения в HEVC-системе, как уже было сказано, осуществляется поблочно. Разбиение видеокадра на блоки производится адаптивно, то есть подстраивается под характер изображения. Прежде всего изображение слева-направо и сверху-вниз разбивается на одинаковые квадратные блоки, назывемые LCU (от англ. Largest Coding Unit). Размер LCU является параметром настройки кодирующей системы и задается перед кодированием. Этот размер может принимать значения 8x8, 16x16, 32x32 и 64x64. Каждый блок LCU может быть разбит на 4 квадратных подблока CU, каждый из которых, в свою очередь, может быть также разбит. Таким образом, LCU является корнем квадродерева. Минимальный размер CU или глубина квадродерева также является задаваемым параметром настройки кодирующей системы и может принимать значения 8x8, 16x16, 32x32, 64x64. Пространственное Intra-предсказание в HEVC выполняется для блоков квадратной формы, называемых PU (от англ. Prediction Unit). Размер PU совпадает с размером CU с двумя исключениями. Во-первых, размер PU не может превышать 32x32. Таким образом, CU с размером 64x64 содержит внутри себя 4 PU с размерами 32x32. Во-вторых, CU нижнего уровня квадродерева, имеющие минимально разрешенный размер, также могут быть разбиты на 4 квадратных PU с вдвое меньшими размерами. В результате набор разрешенных в HEVC размеров PU состоит из следующих значений: 4x4, 8x8, 16x16, 32x32. Пример разбиения изображения на блоки CU и PU приведен на рис. 1. Более толстой сплошной линией выделены границы LCU. Границы подблоков CU отмечены тонкой сплошной линией. Пунктиром обозначены границы PU в тех случаях, когда CU содержит 4 PU. Здесь же цифрами внутри блоков указан порядок перебора PU при кодировании.

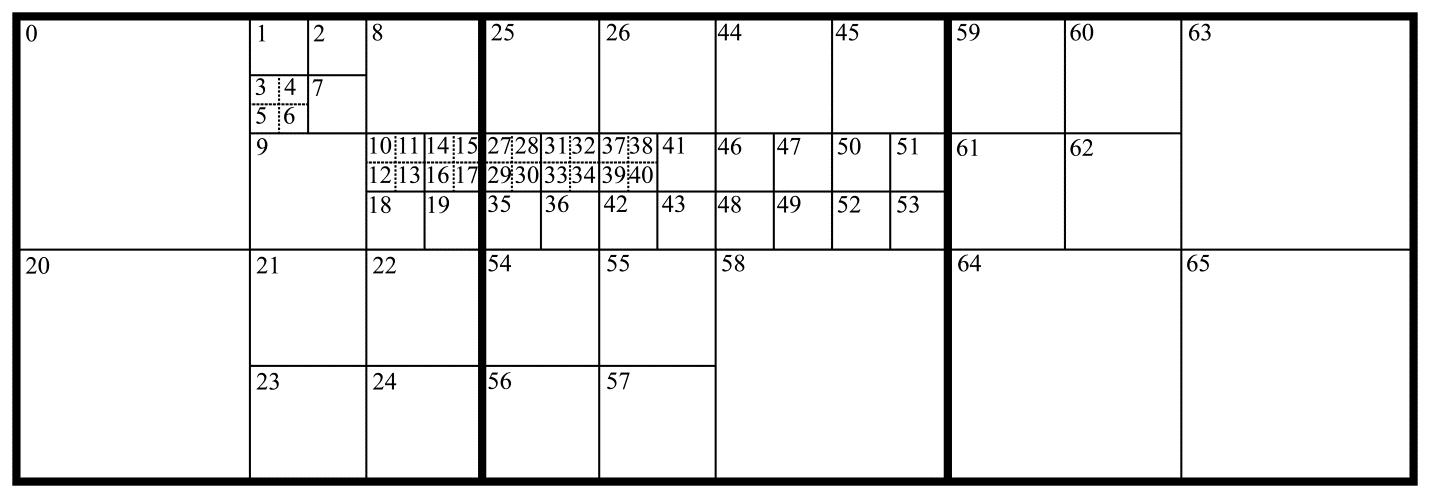
Рис.1. Границы LCU, CU и PU (жирные сплошные линии, тонкие сплошные линии и пунктирные линии соответственно), а также порядок перебора блоков при кодировании (цифры внутри блоков)

При пространственном предсказании значений пикселов внутри текущего кодируемого блока в HEVC используются значения пикселов блоков, соседних с кодируемым. Эти пикселы называют референсными. Расположение референсных пикселов относительно кодируемого блока иллюстрируется на рис. 2. На этом рисунке текущий кодируемый блок помечен буквой C (его размер в этом примере составляют 8x8 отсчетов). Буквами A, B, D, E, F отмечены блоки, содержащие референсные пикселы. Их расположение отмечено серым цветом. Отметим, что далеко не всегда все референсные пикселы доступны для использования при предсказании. Очевидно, что для блоков с номерами 0, 1, 2, 8 на рис. 1 пикселы из блоков D, A, B недоступны, т. к. блоки с этими номерами находятся в самом верху видеокадра. Но это не единственный вариант, когда референсные пикселы считаются недоступными. Стандартом разрешено использовать для предсказания только те референсные пикселы, которые относятся к уже закодированным блокам. Такое ограничение позволяет после кодирования каждого блока произвести его декодирование и уже декодированные пикселы использовать в качестве референсных. Таким образом обеспечивается идентичность результатов предсказания в кодирующей и декодирующей системах. Для примера рассмотрим доступность референсных пикселов для блока с номером 17 на рис. 1. При предсказании этого блока доступными оказываются только пикселы из блоков A, D, E. Остальные блоки, окружающие блок номер 17 при заданном порядке обхода еще не подвергались процедуре кодирования и, как следствие, не могут использоваться при предсказании.

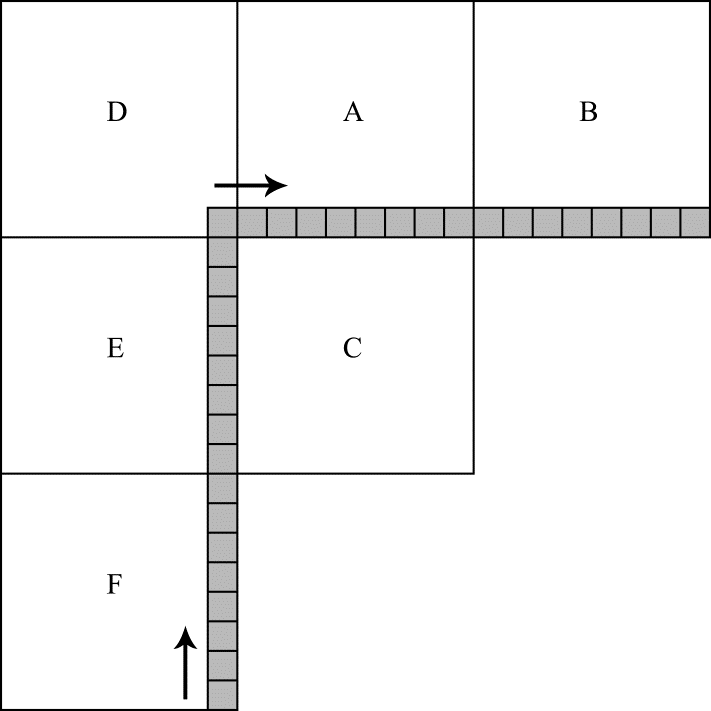
Рис.2. Расположение референсных пикселов относительно кодируемого блока

Всего в HEVC предусмотрено 35 различных вариантов расчета значений отсчетов в кодируемой области по значениям референсных пикселов при пространственном предсказании. Эти варианты называют режимами предсказания (Prediction modes). Каждый режим идентифицируется своим номером в диапазоне от 0 до 34.

В целом, в процедуре пространственного предсказания можно выделить четыре этапа. Те или иные из этих этапов не выполняются для некоторых режимов предсказания и размеров кодируемого блока. Первый этап заключается в генерации значений недоступных референсных пикселов, и он выполняется всегда, когда недоступные отсчеты есть. Сама генерация очень проста. Все недоступные значения приравниваются значению первого доступного отсчета. Так, например, если недоступны блоки D, A, B (рис. 2), то значения всех референсных пикселов из этих блоков устанавливаются равными значению самого верхнего референсного отсчета из блока E. Если недоступен блок B, то вся линейка значений отсчетов этого блока устанавливается равной значению самого правого референсного пиксела из блока A. Этап генерации для вертикальной линейки недоступных референсных отсчетов выполняется симметрично. Наконец, в том случае, когда ни один из блоков A, B, D, E, F недоступен, значения всех референсных отсчетов устанавливаются равными половине от максимально возможного значения. То есть, если кодируется видео, в котором отсчеты представляются 8-разрядными числами, то в этом случае всем референсным пикселам присваивается значение 127.

На втором этапе предсказания последовательность референсных отсчетов, перебираемых сначала снизу-вверх (то есть начиная с нижнего отсчета в блоке F и заканчивая отсчетом в блоке D), а затем слева-направо (то есть начиная с левого отсчета в блоке A и заканчивая самым правым отсчетом в блоке B), подвергается фильтрации. Направление перебора отсчетов при фильтрации отмечено на рис. 2 стрелками. Тип фильтра определяется размерами кодируемого блока. Для некоторых номеров режимов предсказания этот этап не выполняется. Кроме того, не выполняется фильтрация и при предсказании блоков размером 4x4.

На третьем этапе производится собственно расчет значений пикселов внутри кодируемого блока. Так как алгоритмы расчета сильно различаются для разных режимов предсказания, рассмотрим их более детально. Для рассмотрения нам понадобятся элементарные знания по математике (в частности тригонометрия).

Введем обозначения. За $\displaystyle N $ обозначим размер кодируемого блока. Предсказываемые значения будем обозначать $\displaystyle p(x,y) $, где под x и y будем понимать координаты предсказываемого пиксела внутри кодируемого блока. Левый верхний отсчет в блоке имеет координаты (0,0). Правый нижний – $\displaystyle ( N-1,N-1) $. Последовательность референсных отсчетов, находящихся над кодируемым блоком (в блоках D, A, B на рис. 2), обозначим за $\displaystyle t( x) $, где координата $\displaystyle x $ может принимать значения -1, 0, 1, … $\displaystyle ...2N-1 $. Столбец же референсных отсчетов, находящихся слева от кодируемого блока обозначим $\displaystyle l(y) $, где координата y также может меняться в диапазоне от -1 до $\displaystyle ...2N-1 $. Введенные обозначения иллюстрируются на рис. 3.

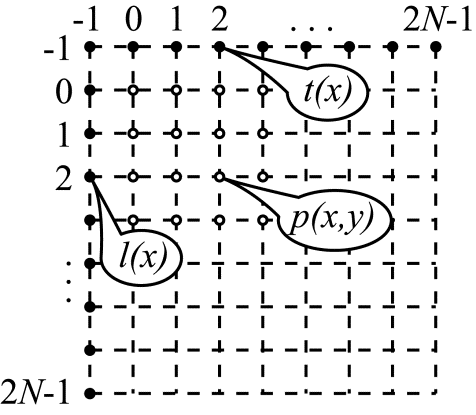
Рис.3. Обозначения, используемые при описании режимов Intra предсказания

Как уже было сказано, каждый режим предсказания однозначно идентифицируется своим номером. Пойдем последовательно по возрастанию номеров.

Режим с номером 0.

Это так называемый DC режим. При использовании этого режима всем отсчетам $\displaystyle p(x,y) $ присваивается одно и то же значение $\displaystyle V_{DC} $ , которое рассчитывается как среднее арифметическое референсных отсчетов:

\begin{array}{l} V_{DC} =\left\lfloor \frac{1}{2N}\left(\sum _{x=0}^{N-1} t( x) +\sum _{y=0}^{N-1} l( x) +N\right)\right\rfloor \\\end{array}

где за $\displaystyle\lfloor .\rfloor $  обозначена операция взятия целой части числа.

Режим с номером 1.

Его также называют Planar. В этом режиме каждое значение $\displaystyle p(x,y) $ получается как среднее арифметическое двух чисел $\displaystyle h( x,y) \  $ и $\displaystyle v( x,y) \  $. Эти числа рассчитывают как результат линейной интерполяции в горизонтальном $\displaystyle ( h( x,y)) $ и вертикальном $\displaystyle ( v( x,y)) $ направлениях. Процессы интерполяции иллюстрируются на рис. 4.

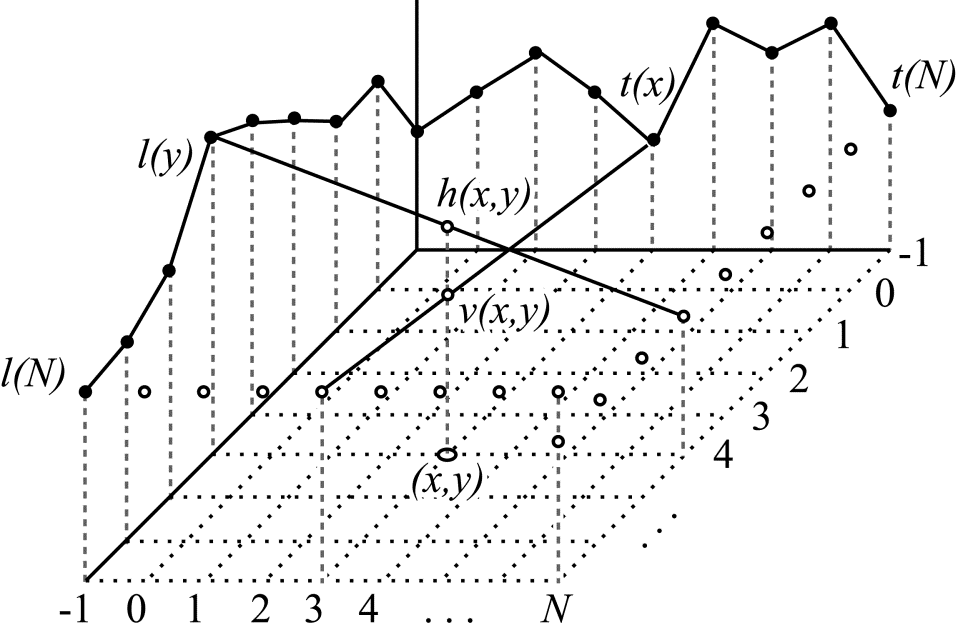
Рис.4. Интерполяция в горизонтальном и вертикальном направлениях

При вычислении $\displaystyle h( x,y) \  $ интерполяция в горизонтальном направлении производится между значением $\displaystyle l(y) $ и отстоящим от него на $\displaystyle N+1 $ отсчетов значением $\displaystyle t(N) $. Значение $\displaystyle v( x,y) \  $ получается в результате интерполяции между значением $\displaystyle t(x) $ и значением $\displaystyle l(N) $, также отстоящим от верхней строки референсных пикселей на $\displaystyle N+1 $ отсчет в вертикальном направлении.
Математически расчет значений в этом режиме можно описать следующим образом:

\begin{array}{l} p( x,y) =\left\lfloor \frac{h( x,y) +v( x,y) +N}{2N}\right\rfloor \\\end{array}

где

\begin{array}{l} h( x,y) =( N-1-x) l( y) +( x+1) t( N) \\\end{array}

а

\begin{array}{l} v( x,y) =( N-1-y) t( x) +( y+1) l( N) \\\end{array}

Остальные режимы предсказания с номерами от 2 до 34 называют угловыми. В этих режимах значения референсных отсчетов в заданном направлении расставляются внутри кодируемого блока. В том случае, когда позиция предсказываемого пиксела $\displaystyle p(x,y) $ попадает между референсными отсчетами, в качестве предсказания используется интерполированное значение. Среди этих режимов можно выделить две симметричные группы. Для режимов с номерами от 2 до 17 расстановка референсных значений производится в направлениях слева-направо. Для режимов с номерами от 18 до 34 такая расстановка ведется сверху-вниз. Соответствие между номерами режимов и направлением расстановки референсных отсчетов иллюстрируется на рис. 5.

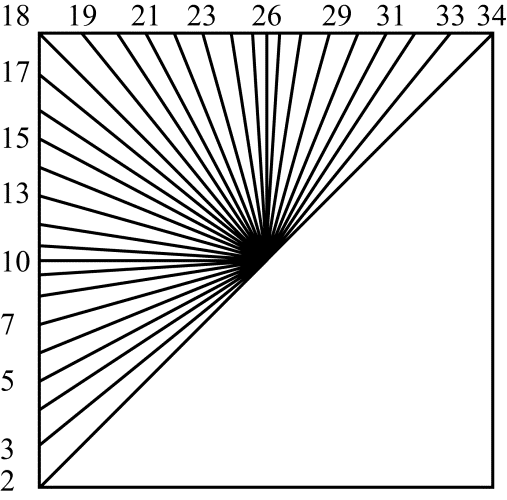
Рис.5. Номера угловых режимов предсказания и соответствующие им направления расстановки референсных отсчетов внутри кодируемого блока

Угловые режимы предсказания с номерами 18-34.

Для этих режимов угол $\displaystyle \varphi \ $, задаваемый номером режима предсказания и определяющий направление расстановки, отсчитывается от вертикального направления (рис. 6). Номерам режимов с 18 по 25 соответствуют отрицательные значения угла $\displaystyle \varphi \ $, номерам с 27 по 34 – положительные.

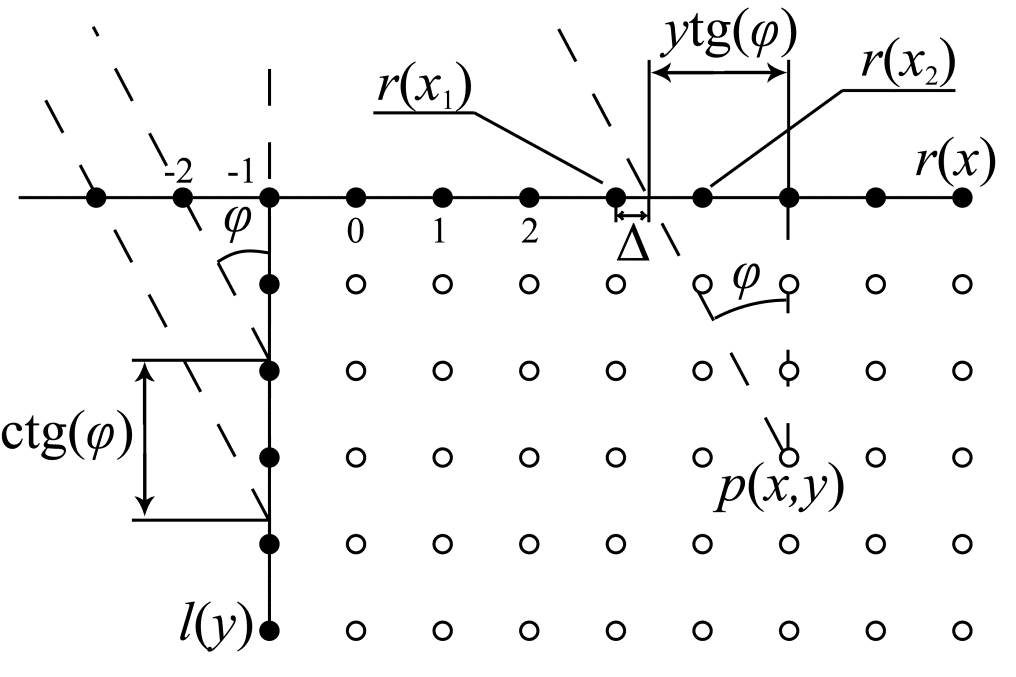
Рис.6. Угловое предсказание в вертикальном направлении

Рассмотрим расчет значения $\displaystyle p(x,y) $, ориентируясь на рис. 6. Очевидно, что координата проекции точки $\displaystyle( x,y) $ на горизонтальную ось, содержащую референсные отсчеты (на рис. 6) обозначены за $\displaystyle r( x) $, но об этом позже), в направлении, задаваемом углом $\displaystyle \varphi \ $, может быть определена как:

\begin{array}{l} \ x\prime =x+y\tan( \varphi ) \\\end{array}

В том случае, когда значение $\displaystyle x\prime $ совпадает с координатой одного из референсных отсчетов, значение $\displaystyle r( \ x\prime ) $ присваивается $\displaystyle p(x,y) $. Это происходит всегда, когда координата проекции $\displaystyle x\prime $ является целым числом. Если $\displaystyle x\prime $ не является целым, то в качестве $\displaystyle p(x,y) $ принимается результат линейной интерполяции между значениями референсных отсчетов $\displaystyle r( x_{1}) $ и $\displaystyle r( x_{2}) $, являющихся соседями точки с координатой $\displaystyle x\prime $. Весовые множители при линейной интерполяции для значений $\displaystyle r( x_{1}) $ и $\displaystyle r( x_{2}) $, т.е. величина $\displaystyle 1-\vartriangle $ и $\displaystyle \vartriangle $, рассчитываются с точностью в $\displaystyle 1/32 $ пиксела*. Все вычисления производятся в целых числах. Для реализации целочисленной арифметики при сохранении заданной точности весовые множители умножаются на 32 перед вычислениями. После проведения расчетов интерполированное значение делится на 32, округляется до ближайшего целого и присваивается $\displaystyle p(x,y) $. Для ускорения расчетов округленные значения $\displaystyle 32\tan( \varphi ) $ для всех значений углов $\displaystyle \varphi \ $ занесены в таблицу (в < arel="nofollow" href="https://www.itu.int/rec/T-REC-H.265">стандарте величина $\displaystyle 32\tan( \varphi ) $ названа intraPredAngle, а ее значения содержатся в таблице 8.4).

Обратим внимание еще на один момент, связанный с угловыми предсказаниями в вертикальном направлении. При отрицательных углах (как раз такой случай изображен на рис. 6) для предсказания необходимо использование референсных отсчетов из вертикального столбца $\displaystyle l(y) $. Для упрощения их использования и вводится вспомогательный массив $\displaystyle r( x) $, значения которого использовались в предыдущих рассуждениях. Необходимость возникает в тех случаях, когда координата проекции $\displaystyle x\prime \ $ имеет отрицательное значения. Номера референсных отсчетов $\displaystyle y\prime \ $ из столбца $\displaystyle l(y) $, которые используются в этом случае определяются величиной угла $\displaystyle \varphi \ $, точнее величиной $\displaystyle\cot( \varphi ) $:

\begin{array}{l} y\prime =x\cot( \varphi ) \\\end{array}

Вычисление значений $\displaystyle y\prime \ $ производится с использованием целочисленной арифметики с точностью до $\displaystyle 1/256 $ отсчета. Для ускорения вычислений округленные значения $\displaystyle 256\cot( \varphi ) $  для всех возможных углов (режимов углового предсказания) рассчитаны заранее и занесены в таблицу (в стандарте величина $\displaystyle 256\cot( \varphi ) $ названа invAngle, а ее значения содержатся в таблице 8.5). Таким образом, перед проведением предсказания при отрицательных углах необходимо рассчитать все возможные значения $\displaystyle y\prime \ $ и занести величины $\displaystyle l( y\prime ) $ в массив $\displaystyle r( x) $ для отрицательных значений $\displaystyle x $. При положительных $\displaystyle x $ значения $\displaystyle r( x) $ совпадают со значениями $\displaystyle t( x) $.

Угловое предсказание в горизонтальном направлении (режимы с номерами 2 – 17) осуществляется аналогично. Угол  в этом случае отсчитывается от горизонтального направления. При этом режимы предсказания с номерами 2 – 9 соответствуют положительным значениям угла $\displaystyle \varphi \ $, а у режимов с номерами 11 – 17 значения $\displaystyle \varphi \ $ отрицательны. Можно даже использовать описанную выше процедуру для предсказания в вертикальных направлениях. Для этого необходимо поменять местами $\displaystyle l(y) $ и $\displaystyle t(x) $, а после расчета квадратной матрицы всех значений $\displaystyle p(x,y) $ провести ее транспонирование.

Как уже было сказано, процедуру пространственного предсказания условно можно разделить на 4 этапа, из которых 3 мы уже рассмотрели. На четвертом этапе предсказанные значения $\displaystyle p(x,y) $ подвергаются дополнительной постфильтрации. Фильтрация четвертого этапа используется только для 3 из 35 режимов предсказания. Это режимы с номерами 0 (DC), 10 (в этом режиме референсные отсчеты, находящиеся слева от кодируемого блока расставляются внутри блока в горизонтальном направлении слева-направо), 26 (в этом режиме референсные отсчеты дублируются внутри блока сверху-вниз). При предсказании с этими режимами на границе блока может возникать резкий перепад между референсными отсчетами и предсказанными значениями. Для режима DC такой перепад может возникать как на левой, так и на верхне границах. Как следствие, процедуре фильтрации подвергаются отсчеты, находящиеся на этих границах. При использовании 10 режима перепад возможен только на верхней границе блока. Соответственно и фильтруются только граничные отсчеты сверху. При использовании режима 26 можно ожидать перепад на левой границе блока, отсчеты которой и подвергаются сглаживанию.

*Примечание. Линейная интерполяция.

Процедура линейной интерполяции на плоскости заключается в том, чтобы по заданной координате $\displaystyle x $ найти значение координаты $\displaystyle y $ для точки $\displaystyle ( x,y) $, расположенной на прямой, соединяющей две заданные точки с координатами $\displaystyle ( x_{1} ,y_{1}) $ и $\displaystyle ( x_{2} ,y_{2}) $. Уравнение прямой, проходящей через две заданные точки $\displaystyle ( x_{1} ,y_{1}) $ и $\displaystyle ( x_{2} ,y_{2}) $ можно записать в виде:

\begin{array}{l} \frac{x -x_{1}}{x_{2} -x_{1}} =\frac{y-y_{1}}{y_{2} -y_{1}} \\\end{array}

Из этого уравнения легко получить:

\begin{array}{l} y=\frac{x-x_{1}}{x_{2} -x_{1}} y_{2} +\left( 1-\frac{x-x_{1}}{x_{2} -x_{1}}\right) y_{1} \\\end{array}

В случае интерполяции между двумя соседними точками дискретной последовательности отсчетов расстояние между соседними отсчетами равно 1. С учетом этого, обозначив за $\displaystyle \vartriangle $ величину $\displaystyle \vartriangle =x-x_{1} $, получим:

\begin{array}{l} y=\vartriangle \cdot y_{2} +( 1-\vartriangle ) y_{1} \\\end{array}

29 ноября 2018

Читать другие статьи:

Глава 1. Просто о видеокодировании

Глава 2. Межкадровое (Inter) предсказание в HEVC

Глава 4. Компенсация движения в HEVC

Глава 5. Постпроцессинг в HEVC

Глава 6. Контекстно-адаптивное двоичное арифметическое кодирование. Часть 1

Глава 7. Контекстно-адаптивное двоичное арифметическое кодирование. Часть 2

Глава 8. Контекстно-адаптивное двоичное арифметическое кодирование. Часть 3

Глава 9. Контекстно-адаптивное двоичное арифметическое кодирование. Часть 4

Глава 10. Контекстно-адаптивное двоичное арифметическое кодирование. Часть 5

Автор:

Олег Пономарев - 16 лет занимается вопросами видео кодирования и цифровой обработки сигналов, специалист в области распространения радиоволн, статистической радиофизики, доцент кафедры радиофизики НИ ТГУ, кандидат физико-математический наук. Руководитель исследовательской лаборатории Elecard.

Инструмент для детального анализа этапов кодирования видеопоследовательности - Elecard StreamEye

Инструмент для сравнения параметров видео, закодированного разными энкодерами