ГЛАВА 9

Процедура бинаризации в частном случае, когда кодирование выполняется только в режиме Intra-предсказания.
Прежде чем переходить к анализу значения оставшихся двух слов в названии энтропийного кодера (Context Adaptive Binary Arithmetic Coding, жирным начертанием выделены два оставшиеся слова), используемого в HEVC, необходимо закончить со словом Binary. Вернемся к схеме алгоритмов кодирования, представленной на рис. 1 Главы 6. На вход энтропийного кодера подается информация, о всех решениях, принятых при кодировании в каждом блоке, присутствующем на схеме. Большая часть этой информации представлена целыми числами, а не бинами, принимающими значения 0 или 1. Да, конечно, любое целое число можно представить в двоичном виде и получить, таким образом, поток бинов на входе энтропийного кодера. Однако, при таком подходе вероятности появления нулей и единиц в двоичном сообщении будут практически равны. В таких условиях степень сжатия данных в арифметическом кодере будет практически равна нулю. Т.е. в результате арифметического кодирования количество битов в закодированном сообщении будет не меньше, чем количество бинов на входе кодера. В связи с этим в HEVC предусмотрена специальная процедура, которой подвергается вся числовая информация, поступающая на вход арифметического кодера. Эта процедура называется бинаризацей. Именно благодаря ей все числовые значения, описывающие процесс кодирования того или иного блока изображения, переводятся в набор двоичных бинов. Рассмотрим детально процедуру бинаризации в частном случае, когда кодирование выполняется только в режиме Intra-предсказания.
Вспомним, что кодирование видеокадра в HEVC осуществляется поблочно в порядке слева-направо и сверху-вниз. Блоки кодирования, называемые LCU, представляют собой квадратные неперекрывающиеся области, равномерно покрывающие всю площадь видеоизображения. Каждый блок при кодировании может быть разбит на 4 квадратных подблока, называемых CU. Каждый из блоков CU, в свою очередь, может быть разбит на 4 квадратных CU меньшего размера. В результате таких разбиений исходный блок LCU размера $\displaystyle 2^{M}$ представляется в виде квадродерева, называемого CTU. Максимальная глубина квадродерева является параметром кодирующей системы. Кроме того, в стандарте задан минимально возможный размер CU, равный 8.
На следующем этапе кодирования для всех CU, являющихся «листьями» квадродерева, выполняется пространственное предсказание. Область, для которой выполняется предсказание, называют блоком предсказания или PU. Здесь возможны два варианта. CU может содержать один блок PU, так что размеры областей CU и PU совпадают, или CU может содержать 4 квадратных PU вдвое меньшего размера. Последний вариант возможен только в том случае, если данный блок CU находится на максимально возможной глубине квадродерева. Само предсказание для каждой области PU может выполняться одним из 35 заданных в стандарте способов. Предсказание для значений яркостной и цветоразностных компонент, представляющих каждый пиксел изображения в предсказываемой области, выполняется по отдельности. Способ предсказания цветоразностных компонент может отличаться от способа предсказания яркостной компоненты. Предсказанные значения вычитаются из значений компонент отсчетов кодируемого изображения, в результате чего формируется двумерный разностный сигнал.
Отсчеты разностного сигнала, сформированного на этапе пространственного предсказания для всего CU, на следующем этапе кодирования поблочно подвергаются двумерному спектральному преобразованию. Блоки разностного сигнала, подвергаемые спектральному преобразованию, называют TU. TU верхнего уровня совпадают по размеру с содержащим его CU. При кодировании TU могут разбиваться на 4 квадратных подблока вдвое меньшего размера. Каждый из таких подблоков, в свою очередь, может быть также разбит. В результате образуется квадродерево, «листья» которого и являются блоками разностного сигнала для спектрального преобразования. Минимальный размер TU задан в стандарте равным 4, максимальный – 32. Полученные в результате спектрального преобразования спектральные отсчеты подвергаются процедуре квантования. Шаг квантования Δ определяется значением параметра квантования Qp: $\displaystyle \Delta =2^{\frac{Q_{p} -4}{6}}$.
Все значения, описывающие выбранный при кодировании вариант разбиения LCU на CU, PU, TU, выбранный способ предсказания для каждого блока PU, значения, полученные в результате квантования спектральных отсчетов разностного сигнала, и т.д. называют синтаксическими элементами. Совокупность синтаксических элементов, относящихся к текущему CU, полностью описывает результат выбранного варианта кодирования изображения в этом блоке. Именно этот набор проходит перед энтропийным кодированием через процедуру бинаризации, отображающей значение каждого синтаксического элемента в набор двоичных символов – бинов. Ниже приведен краткий перечень типов синтаксических элементов, используемых при описании кодируемого изображения в HEVC при пространственном предсказании, а также алгоритмы их бинаризации. В перечне мы использовали те же названия синтаксических элементов, что и в спецификации стандарта H.265/HEVC.
Разбиение LCU на блоки CU меньшего размера, т.е. структура квадродерева CU, индицируется в потоке синтаксическим элементом split_cu_flag. Этот синтаксический элемент может принимать два значения: 0 – в том случае, если текущая CU не разбивается на меньшие блоки; 1 – в обратном случае. Двоичное значение split_cu_flag непосредственно поступает на вход энтропийного кодера минуя процедуру бинаризации.
Следующий синтаксический элемент – part_mode – присутствует в описании CU в том случае, если при построении квадродерева достигнута максимально возможная глубина разбиений. Элемент part_mode может принимать только два значения. Значение part_mode = 1 индицирует случай, когда размеры PU и CU совпадают. При part_mode = 0 блок CU содержит 4 квадратных блока PU вдвое меньшего размера. Процедура бинаризации для значений этого синтаксического элемента сводится к инверсии его двоичного значения.
Для определения способа пространственного предсказания яркостной компоненты пикселов блока PU (одного из 35) используются значения трех синтаксических элементов: prev_intra_luma_pred_flag, mpm_idx и rem_intra_luma_pred_mode. Бинарный синтаксический элемент prev_intra_luma_pred_flag=1, если номер режима предсказания должен вычисляться по номерам режимов предсказания соседних блоков PU (соседними блоками считаются два блока, примыкающие к текущему слева и сверху). В результате вычислений получаются три возможных значения. Выбор из полученных трех значений индицируется синтаксическим элементом mpm_idx = 0, 1, 2. При prev_intra_luma_pred_flag = 0 номер способа пространственного предсказания не является ни одним из трех рассчитанных значений. В этом случае выбор одного из оставшихся 32 способов предсказания осуществляется с помощью 5-разрядного синтаксического элемента rem_intra_luma_pred_mode.
Бинарное значение prev_intra_luma_pred_flag не подвергается бинаризации. При бинаризации значение mpm_idx=0 отображается в один нулевой бин. Значение mpm_idx=1 отображается в последовательность из двух бинов 10. Значение mpm_idx=2 – в последовательность из двух бинов 11.
Бинаризация rem_intra_luma_pred_mode отображает его значение в последовательность из 5 бинов, дающих двоичное представление значения синтаксического элемента.
Номер способа предсказания цветоразностных компонент блока PU индицируется в потоке синтаксическим элементом intra_chroma_pred_mode, который может принимать значения от 0 до 4. В случае, когда intra_chroma_pred_mode=4, способ предсказания цветоразностных компонент совпадает со способом предсказания яркостной компоненты. Для остальных четырех значений этого синтаксического элемента соответствующие номера способов предсказания заданы в стандарте HEVC таблично. При бинаризации значение intra_chroma_pred_mode=4 отображается в один бин со значением 0. Остальные значения intra_chroma_pred_mode процедура бинаризации отображает в последовательность из 3 бин, первый из которых всегда равен 1, а остальные два являются двоичным представлением значения intra_chroma_pred_mode.
Разбиение блока CU на квадратные блоки TU, т.е. структура квадродерева блоков TU, индицируется в потоке синтаксическим элементом split_transform_flag. Если этот синтаксический элемент равен 0, то размер блока разностного сигнала, подвергаемого спектральному преобразованию, совпадает с размером блока CU. В противном случае блок TU разбивается на 4 квадратных блока вдвое меньшего размера. Двоичное значение split_transform_flag не подвергается бинаризации.
Три синтаксических элемента cbf_cb, cbf_cr и cbf_luma показывают, содержит ли блок TU ненулевые значения спектральных отсчетов для цветоразностных и яркостной компонент разностного сигнала. Значения этих трех синтаксических элементов не требуют бинаризации.
При отличии от 0 флагов cbf_cb, cbf_cr и cbf_luma в потоке присутствует описание соответствующего блока спектральных отсчетов. Это описание выполняется с помощью восьми различных синтаксических элементов: last_sig_coeff_x, last_sig_coeff_y, coded_sub_block_flag, sig_coeff_flag, coeff_abs_level_greater1_flag, coeff_abs_level_greater2_flag, coeff_sign_flag, coeff_abs_level_remaining. Описание блока TU начинается с двух синтаксических элементов last_sig_coeff_x и last_sig_coeff_y. Значения этих элементов определяются координатами (x, y) последнего ненулевого спектрального отсчета в блоке TU при заданном порядке обхода спектральных отсчетов. При обходе блок TU разбивается на подблоки размером $\displaystyle 4\times 4$. Порядок обхода подблоков внутри блока TU и коэффициентов внутри каждого подблока совпадают. Для TU с размерами $\displaystyle 4\times 4$ и $\displaystyle 8\times 8$ возможны три варианта обхода: диагональный, горизонтальный и вертикальный. Тот или иной вариант определяется номером режима предсказания. Для блоков TU больших размеров возможен только диагональный порядок обхода. Три варианта обхода для блока TU размером $\displaystyle 8\times 8$ иллюстрируются на рис. 1.

Figure 1. Три варианта обхода блоков размером $\displaystyle 4\times 4$ в блоке TU размером $\displaystyle 8\times 8$ и коэффициентов внутри каждого блока размером $\displaystyle 4\times 4$. Диагональный порядок обхода блоков (а), коэффициентов (б). Горизонтальный порядок обхода блоков (в), коэффициентов (г).Вертикальный порядок обхода блоков (д), коэффициентов (е)
Дальнейшее описание блока TU происходит по подблокам в порядке, задаваемом направлением обхода. Первым производится описание подблока, содержащего позицию (last_sig_coeff_x, last_sig_coeff_y). Последним описывается подблок, содержащий отсчет с координатами (0,0). Описание каждого подблока начинается с синтаксического элемента coded_sub_block_flag. Значение этого элемента равно 1, если подблок содержит ненулевые спектральные коэффициенты. В противном случае coded_sub_block_flag задается равным нулю и на этом описание данного подблока заканчивается.
Для каждого из подблоков, содержащих ненулевые значения, описание продолжается набором синтаксических элементов sig_coeff_flag. Этот элемент равен 1, если спектральный коэффициент в подблоке отличен от 0. В противном случае значение этого синтаксического элемента равно 0. Порядок перебора спектральных коэффициентов внутри подблока при этом задается направлением обхода. Дальнейшее описание спектральных отсчетов производится только для тех позиций, для которых sig_coeff_flag равен 1. Для этих позиций описание продолжается набором синтаксических элементов coeff_abs_level_greater1_flag, значение которых равно 1, если абсолютное значение соответствующего спектрального элемента больше 1, и равно нулю в противном случае. Для каждого подблока генерируется не более 8 синтаксических элементов этого типа. Порядок генерации задается направлением обхода. Следующий синтаксический элемент – coeff_abs_level_greater2_flag – индицирует позицию первого, в порядке обхода, спектрального отсчета, абсолютное значение которого по величине больше 2. Описание подблока спектральных коэффициентов продолжается последовательностью синтаксических элементов coeff_sign_flag, индицирующих знак (положительный или отрицательный) каждого из спектральных отсчетов отличных от нуля, т.е. только тех, для которых sig_coeff_flag=1. Для положительных отсчетов coeff_sign_flag устанавливается равным 0, для отрицательных – 1. Описание каждого подблока завершается набором значений синтаксических элементов coeff_abs_level_remaining. Значения генерируемых синтаксических элементов определяются разницей:
coeff_abs_level_remaining = |W| - 1 - coeff_abs_level_greater1_flag - coeff_abs_level_greater2_flag,
где $\displaystyle W$ – значение спектрального отсчета. Эти значения присутствуют в описании подблока только для тех позиций, перебираемых в порядке обхода, для которых sig_coeff_flag=1 и сгенерированное значение coeff_abs_level_remaining отлично от нуля. Пример описания подблока спектральных коэффициентов (рис. 2) приведен в Табл. 1 (Пример взят из кники Wien M. High Efficiency Video Coding: Coding Tools and Specification).
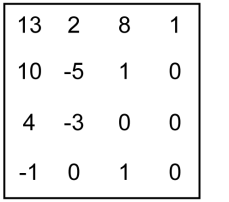
Figure 2. Пример блока квантованных спектральных коэффициентов
Таблица 1
Значения синтаксических элементов при описании блока (рис. 2)
| Значения коэффициентов в порядке обхода | 1 | 0 | 0 | 0 | 1 | 1 | -3 | -1 | 8 | -5 | 4 | 2 | 10 | 13 |
| sig_coeff_flag | - | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| coeff_abs_level_greater1_flag | 0 | - | - | - | 0 | 0 | 1 | 0 | 1 | 1 | 1 | 1 | - | - |
| coeff_abs_level_greater2_flag | - | - | - | - | - | - | 1 | - | - | - | - | - | - | - |
| coeff_sign_flag | 0 | - | - | - | 0 | 0 | 1 | 1 | 0 | 1 | 0 | 0 | 0 | 0 |
| coeff_abs_level_remaining | - | - | - | - | - | - | 1 | - | 7 | 4 | 3 | 1 | 10 | 13 |
Значения last_sig_coeff_x и last_sig_coeff_y при бинаризации отображаются в последовательности бинов, состоящие из двух частей: префиксной и суффиксной. Правила отображения иллюстрируются в таблице 2. В префиксной строке нулевой бин, взятый в скобки во втором столбце таблицы, опускается, если бинаризируемое значение совпадает с величиной $\displaystyle nT-1$ , где $\displaystyle nT$– размер блока TU. Величины $\displaystyle x_{i}$, из которых состоит суффиксная строка бинов, представляют собой значения i-ых разрядов двоичного представления бинаризируемого числа.
Таблица 2
Бинаризация last_sig_coeff_x и last_sig_coeff_y
| Бинаризируемое значение | Префиксная строка бинов | Суффиксная строка бинов |
| 0 | 0 | |
| 1 | 10 | |
| 2 | 110 | |
| 3 | 111(0) | |
| 4, 5 | 11110 | $\displaystyle x_{0}$ |
| 6, 7 | 11111(0) | $\displaystyle x_{0}$ |
| 8, ..., 11 | 1111110 | $\displaystyle x_{1} x_{0}$ |
| 12, ..., 15 | 1111111(0) | $\displaystyle x_{1} x_{0}$ |
| 16, ..., 23 | 11111111 | $\displaystyle 0\ x_{2} x_{1} x_{0}$ |
| 24, ..., 31 | 11111111 | $\displaystyle1\ x_{2} x_{1} x_{0}$ |
Значения всех одноразрядных синтаксических элементов, используемых при описании подблока спектральных коэффициентов (coded_sub_block_flag, sig_coeff_flag, coeff_abs_level_greater1_flag, coeff_abs_level_greater2_flag, coeff_sign_flag) не требуют бинаризации
Значения синтаксического элемента coeff_abs_level_remaining отображаются при бинаризации в две последовательности бинов: префиксную и суффиксную. Процедура бинаризации параметризована. Значение параметра бинаризации k определяется по величине предыдущих (бинаризированных ранее) значений синтаксических элементов coeff_abs_level_remaining в данном подблоке. Примеры результатов бинаризации при двух значениях k приведены в таблице 3 (Из книги Wien M. High Efficiency Video Coding: Coding Tools and Specification). За $\displaystyle Z$ в таблице 3 обозначено бинаризируемое значение, а за $\displaystyle x_{i}$ – значения разрядов двоичного представления величины $\displaystyle Z$. Жирным начертанием в таблице выделена префиксная последовательность бинов.
Таблица 3
Примеры бинаризации coeff_abs_level_remaining.
| $\displaystyle Z$ | Примеры бинаризации при $\displaystyle k=0$ | $\displaystyle Z$ | Примеры бинаризации при $\displaystyle k=1$ |
| 0 | $\displaystyle 0$ | 0, 1 | $\displaystyle0\ x_{0}$ |
| 1 | $\displaystyle 10$ | 2, 3 | $\displaystyle10\ x_{0}$ |
| 2 | $\displaystyle 110$ | 4, 5 | $\displaystyle110\ x_{0}$ |
| 3 | $\displaystyle 1110$ | 6, 7 | $\displaystyle1110\ x_{0}$ |
| 4, 5 | $\displaystyle11110\ x_{0}$ | 8, ..., 11 | $\displaystyle11110\ x_{1} x_{0}$ |
| 6, ..., 9 | $\displaystyle111110\ x_{1} x_{0}$ | 12, ..., 19 | $\displaystyle111110\ x_{2} x_{1} x_{0}$ |
| 10, ..., 17 | $\displaystyle1111110\ x_{2} x_{1} x_{0}$ | 20, ..., 35 | $\displaystyle1111110\ x_{3} x_{2} x_{1} x_{0}$ |
17 декабря 2019
Читать другие статьи:
Глава 1. Просто о видеокодировании
Глава 2. Межкадровое (Inter) предсказание в HEVC
Глава 3. Пространственное (Intra) предсказание в HEVC
Глава 4. Компенсация движения в HEVC
Глава 5. Постпроцессинг в HEVC
Глава 6. Контекстно-адаптивное двоичное арифметическое кодирование. Часть 1
Глава 7. Контекстно-адаптивное двоичное арифметическое кодирование. Часть 2
Глава 8. Контекстно-адаптивное двоичное арифметическое кодирование. Часть 3
Глава 10. Контекстно-адаптивное двоичное арифметическое кодирование. Часть 5
Автор:
Олег Пономарев - 16 лет занимается вопросами видео кодирования и цифровой обработки сигналов, специалист в области распространения радиоволн, статистической радиофизики, доцент кафедры радиофизики НИ ТГУ, кандидат физико-математический наук. Руководитель исследовательской лаборатории Elecard.
Инструмент для детального анализа этапов кодирования видеопоследовательности - Elecard StreamEye
Инструмент для сравнения параметров видео, закодированного разными энкодерами